TYPES OF ANGLES
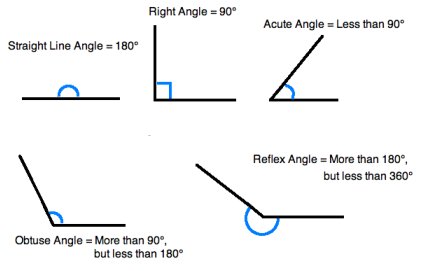
We began our unit with the various types of angles. Students will need to know the various angles and how to measure and draw them.
We began our unit with the various types of angles. Students will need to know the various angles and how to measure and draw them.
MEASURING ANGLES
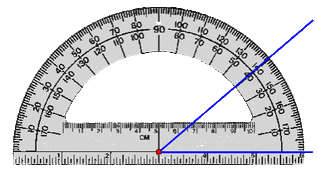
1. Place the vertex at the center of the protractor
2. One arm of the angle lines up with the base line on the protractor
3. Find where the other line of the angle meet the edge of the protractor
Reflex Angles: Measure the inside angle then subtract it from 360.
DRAWING ANGLES
1. Draw a base line with a ruler or edge of the protractor
2. Place the vertex at the center of the protractor
3. Make a dot at the desired degree
4. Connect the vertex and dot drawn at edge of protractor
5. Draw the angle (semi circle or right angle partial square)
1. Draw a base line with a ruler or edge of the protractor
2. Place the vertex at the center of the protractor
3. Make a dot at the desired degree
4. Connect the vertex and dot drawn at edge of protractor
5. Draw the angle (semi circle or right angle partial square)
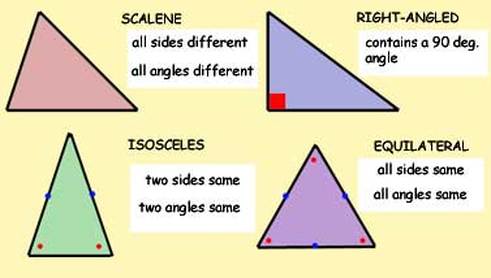
TYPES OF TRIANGLES
We discussed several types of triangles. Students need to know the types and side length/ angles can help us categorize triangles. Students will need to know the difference between the various triangles.
SUM OF INTERIOR ANGLES IN A TRIANGLE
All angles in a triangle when added together will equal 180 degrees. Students tested this theory by cutting the angles off of a triangle and glued them to a straight 180 degree line.
Students need to know how to find the missing angles when confronted with a triangle sum question.
MATH QUIZ:
Students will be having a math quiz on Friday February 6th.
Topics covered will be:
Extra work pages for those that need a little extra help can be found on the homework page.
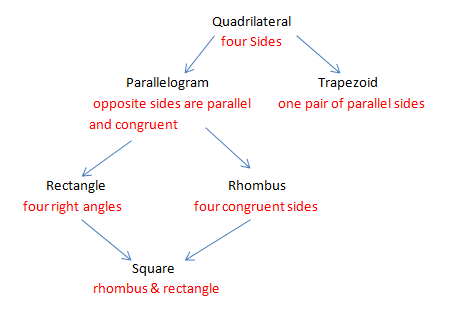
SUM OF INTERIOR ANGLES IN A QUADRILATERAL
All angles in a quadrilateral when added together will equal 360 degrees. Students tested this theory by cutting their four sided shape into two triangles; and we know that the sum of all the angles in a triangle is 180 degrees therefore two triangles would be 360 degrees.
Students need to know how to find the missing angles when confronted with a quadrilateral sum question.
All angles in a triangle when added together will equal 180 degrees. Students tested this theory by cutting the angles off of a triangle and glued them to a straight 180 degree line.
Students need to know how to find the missing angles when confronted with a triangle sum question.
MATH QUIZ:
Students will be having a math quiz on Friday February 6th.
Topics covered will be:
- Types of angles (degrees, description, picture)
- How to draw angles
- How to measure angles
- Type of triangles
- Describing why the angles of a triangle equal 180 degrees
- Determining missing angles in a triangle
Extra work pages for those that need a little extra help can be found on the homework page.
SUM OF INTERIOR ANGLES IN A QUADRILATERAL
All angles in a quadrilateral when added together will equal 360 degrees. Students tested this theory by cutting their four sided shape into two triangles; and we know that the sum of all the angles in a triangle is 180 degrees therefore two triangles would be 360 degrees.
Students need to know how to find the missing angles when confronted with a quadrilateral sum question.
CONSTRUCTING TRIANGLES
Now that students know how to measure angles and the various types of triangles we can now construct triangles based on certain criteria. Below is our Notebook Lesson on this task.
Now that students know how to measure angles and the various types of triangles we can now construct triangles based on certain criteria. Below is our Notebook Lesson on this task.
| Constructing_triangles.notebook | |
| File Size: | 766 kb |
| File Type: | notebook |
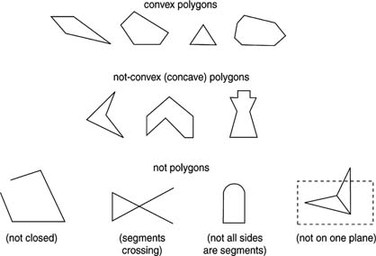
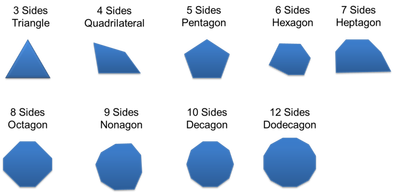
POLYGONS
Polygons can be in many varieties. We focused on: Regular polygons, irregular polygons, convex polygons and concave polygons.
In order for a shape to categorized as a polygon it must be flat (one plane), have only straight edges and angles, and it must be a closed shape.
Polygons can be in many varieties. We focused on: Regular polygons, irregular polygons, convex polygons and concave polygons.
In order for a shape to categorized as a polygon it must be flat (one plane), have only straight edges and angles, and it must be a closed shape.
TYPES OF POLYGONS
| Investigating_polygons.notebook | |
| File Size: | 1360 kb |
| File Type: | notebook |
CONGRUENCE
Two shapes are said to be congruent if they are exactly the same size and shape.
Two shape are said to be similar if they are the same shape but a different size.
Two shapes are said to be congruent if they are exactly the same size and shape.
Two shape are said to be similar if they are the same shape but a different size.
| Congruency_of_polygons.notebook | |
| File Size: | 1254 kb |
| File Type: | notebook |
PERIMETER
The perimeter of a polygon is the distance around the outside of the polygon. Students in the past just added up the outside edges. This year we learned about strategies we could use to make it faster by using a formulas
Square: 4S
Rectangle: 2L + 2W
Regular Polygons: #ofS x L
Irregular Polygons: Add up all edges
The perimeter of a polygon is the distance around the outside of the polygon. Students in the past just added up the outside edges. This year we learned about strategies we could use to make it faster by using a formulas
Square: 4S
Rectangle: 2L + 2W
Regular Polygons: #ofS x L
Irregular Polygons: Add up all edges
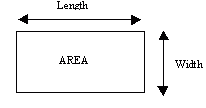
AREA
The area of a polygon is the number of square units in a shape. We measure the area or a rectangle by multiplying the length and height together. A= L x W
The area of a polygon is the number of square units in a shape. We measure the area or a rectangle by multiplying the length and height together. A= L x W
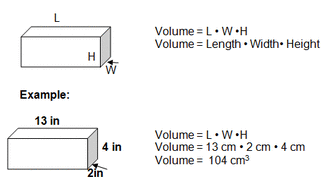
VOLUME
Volume is the amount of space occupied by an object. We calculate the volume of a rectangular prism by multiplying the length x width x height
Volume is the amount of space occupied by an object. We calculate the volume of a rectangular prism by multiplying the length x width x height